图1 基于“高斯网”表示进行高真实感几何变形建模的效果

Part1

问题和背景

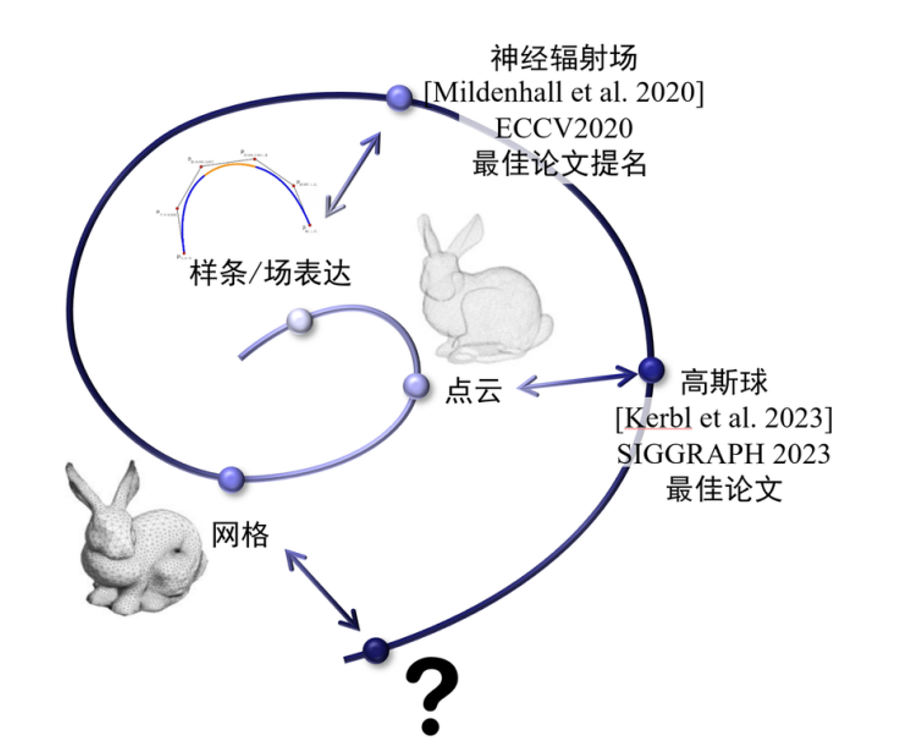
图2 几何表征的发展

变形建模是几何建模的关键技术之一，对不同的几何表征有相应专业的变形方法。网格变形研究历史长，并已经研发出了数据驱动的方法来进行网格建模[2][3]，通过少量的用户交互可以生成大尺度的变形结果。为了对神经辐射场进行变形，在网格变形的基础上，Nerf-Editing[4]通过对光线进行扭曲来达到对神经辐射场进行变形的效果。

近期高斯泼溅(Gaussian Splatting)引起了学术界和工业界的广泛关注，其结合了显式和隐式表示的优势，将三维场景表达为多个三维高斯球函数的组合，每个高斯球函数包含位置、大小、朝向、颜色和不透明度等信息，通过将三维高斯球投影到图像平面上的方式实现三维场景的渲染。

相比于神经辐射场，该三维表示训练开销小，并且基于光栅化技术可以实现高效高质量渲染。然而，由于高斯泼溅使用离散高斯球函数定义，缺乏显式拓扑结构，因此进行大尺度几何变形时容易出现瑕疵(如图3所示)，现有神经辐射场和高斯泼溅的变形方法难以处理高真实感大尺度变形的问题。

(a) NeRF Editing[4]

(b) 3D-GS[8]

(c) SuGaR[6]

图3 现有神经辐射场与高斯泼溅变形方法难以处理大尺度变形

为了解决上述问题，该项研究工作基于高斯泼溅提出了一种高斯网表征方法，在保持高效高质量渲染效果的同时，支持实时大尺度变形建模(如图4所示)。

图4 高斯网新视角合成结果与大尺度变形建模结果

Part 2

方法概述

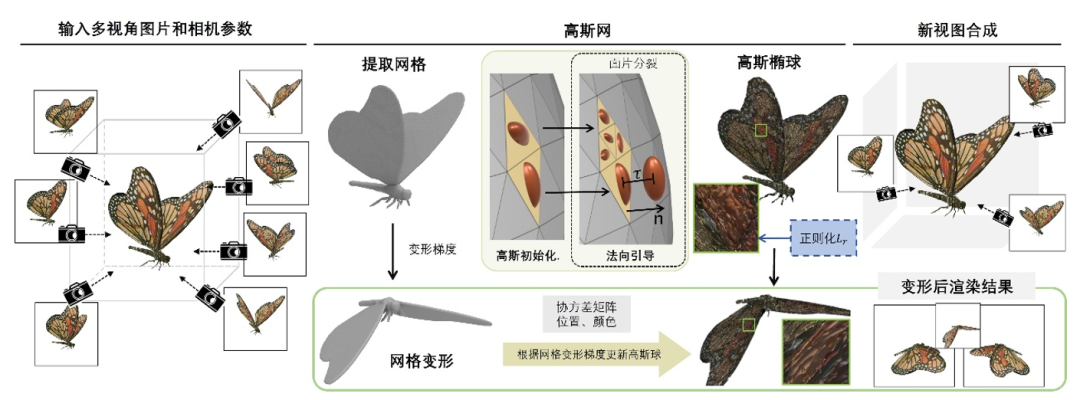
图5 基于网格的高斯泼溅变形方法示意图

该方法提出的高斯网是一种基于网格的高斯泼溅表示方法，它利用重建的网格作为几何先验，并在网格的面上嵌入高斯球，具体表征如图6所示。高斯网在保留原高斯泼溅表示的基础上进行了扩展，具体而言其保留了原有的缩放、旋转、不透明度和颜色等特征；引入了可优化的重心坐标 w = (wa, wb, wc)；利用所在三角形面片的三个顶点坐标 (va, vb, vc) 来表示高斯球的空间坐标。这种表示方法不仅保持了高斯泼溅的优势，还通过与网格表示的结合，提供了更强的几何约束和编辑灵活性。高斯网利用如下的方法进行优化：

1. 法向引导策略。引入可优化的偏移幅度t，代表沿面片法线n的位移。用高斯球所在三角形面片的外接圆半径 r 表示可以沿法向偏移的最大距离。高斯球的空间坐标具体表示如下：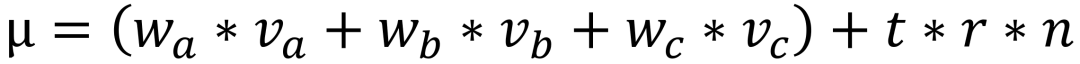

   

2. 面片分裂策略。受到SubdivNet[5]使用三角网格细分[9]进行几何学习的启发，在高斯密度控制阶段中改变了原本的分裂策略。对影响渲染质量的高斯，根据其所绑定的面片进行分裂，即在每个三角形边的中点插入一个新的顶点，单个三角形面片在平面上被细分为四个较小的三角形，高斯球也被分裂为四个，并隶属于每个小三角形的面片。

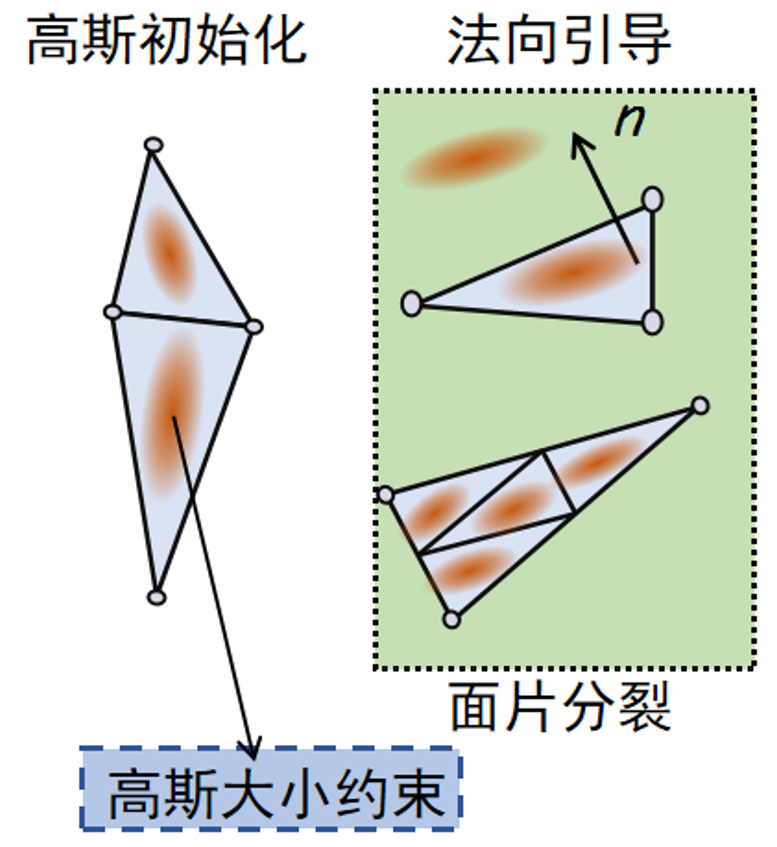
图6 高斯网表征模块示意图

2.2 训练优化模块

高斯网的训练优化过程与传统高斯泼溅方法的训练流程相似，主要包含初始化、优化和密度控制三个主要阶段。在高斯网的初始化过程中，在代理网格的每个面的重心上嵌入一个高斯球，记录高斯球所在面片的重心坐标，其余参数随机初始化。在高斯网的每轮优化迭代过程中，引入正则项，在训练过程中根据邻近三角形的大小调整高斯球形状，确保在变形过程中学习适当的高斯球形状并保持局部连续性。正则化约束为：

其中si是每个高斯分布的三维尺度向量，ri 是高斯分布所在三角形的外接圆半径，γ 是一个来控制相邻三角形对高斯分布大小影响的超参数。在高斯网的密度控制过程中，采用面片分裂策略：每隔一定轮数，对不满足渲染条件的高斯球进行面片分裂，同时将新分裂的面更新到代理网格中。

2.3 变形驱动模块

变形驱动模块如图7所示。在该模块中，首先对代理网格进行变形，用户在对代理网格进行拖拽变形后，根据变形前后的代理网格优化变形能量，提取出网格顶点对应的变形梯度T，对变形梯度进行极性分解可以得到仿射矩阵S 和旋转矩阵R；接着由于高斯网的每个高斯球记录了所附着面片的三个顶点的信息，可以将顶点变形前后的位移和变形梯度传递到附着在网格面片上的高斯球；最后高斯网的每个高斯球借助变形梯度和位移对其协方差矩阵、空间位置和球谐函数的输入视角进行更新，得到变形后高斯球。具体驱动公式如下:

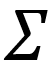其中，和T分别代表每个高斯在变形过程中产生的顶点位移和变形梯度，R由变形梯度极性分解得到。代表高斯变形前的空间位置，代表高斯的协方差矩阵，由旋转和缩放计算得到，SH(*)代表球谐函数，输入相机视角d 和颜色特征c后得到最终的颜色值。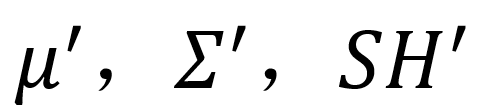均是变形后的高斯属性。

图7 高斯网变形驱动模块示意图

Part 3

结果展示

图8展示了该方法在不同物体上进行变形后的新视角渲染结果。从图示结果可以看出，高斯网这种表示方法能获得高质量的变形后的渲染结果，无尖刺或伪影现象产生。

图8 不同物体在变形后新视角渲染结果

图9展示了高斯网在四种真实场景下的变形建模的结果。每种场景左边展示了变形前的渲染结果，右边展示了变形后的渲染结果。从图示结果可以看出，高斯网可以对复杂的真实场景进行大尺度变形建模，变形后的场景仍保持着高真实感的渲染结果。

图9 真实场景下的变形结果

图10展示了该方法与其他方法在变形上的对比结果，包括神经辐射场的编辑方法NeRF-Editing、直接将高斯球投影到网格上的编辑方法（Baseline）、用高斯重建网格的方法SuGaR，对比结果证明了该方法在大尺度变形上有明显的优势。

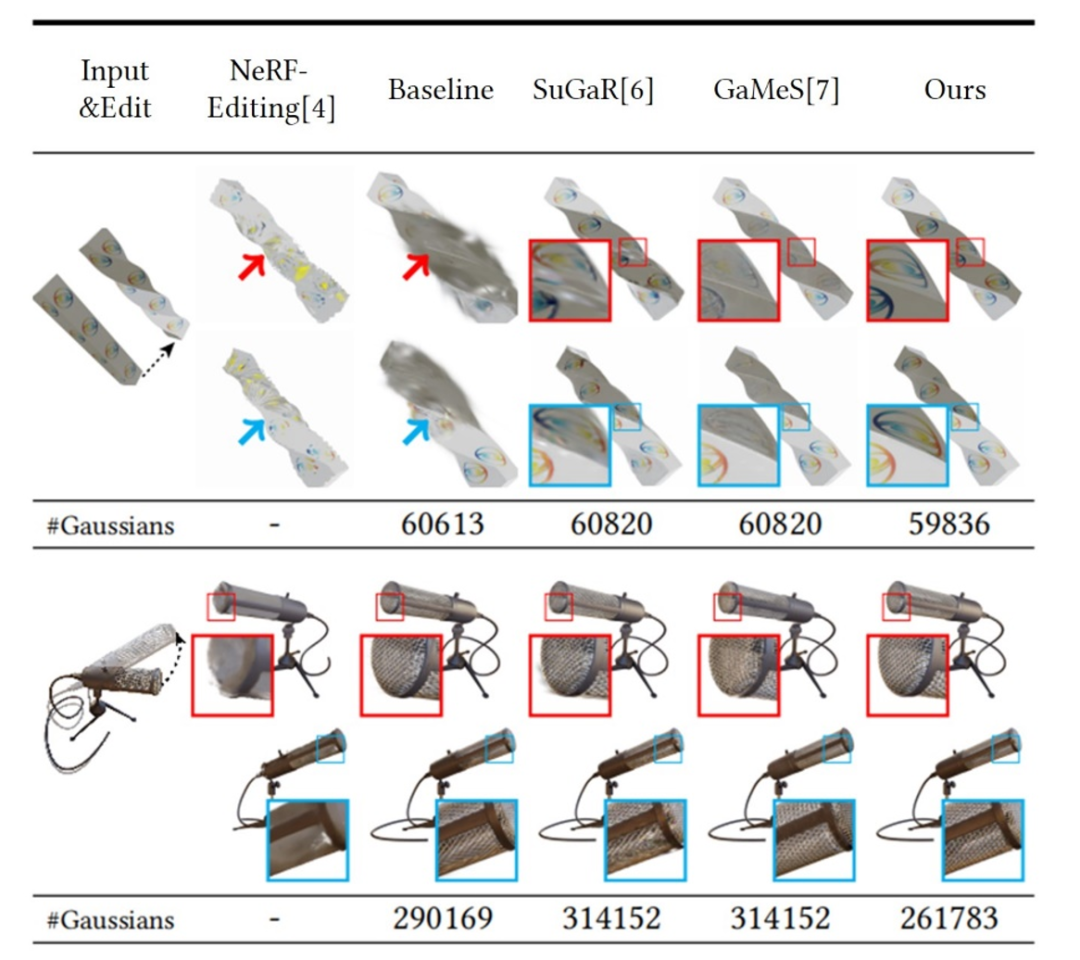
图10 变形后的渲染结果对比

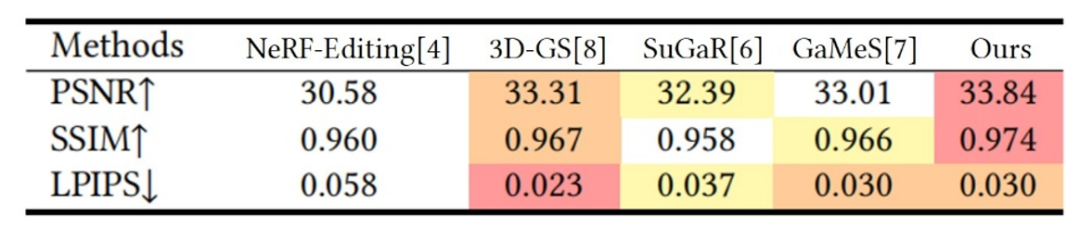
同时，该方法还对新视图的合成质量进行了评估，证明了高斯绑定网格这种表示形式在新视角的合成质量上也能实现较好的效果。

表1 新视图合成量化指标对比

该方法还建立了经典变形方法与高真实感变形建模方法之间的桥梁，基于数据驱动的网格变形方法[4]，可以通过少量的交互变形出具有复杂运动的高斯网模型，如布料等物体的变形。图11展示了基于数据驱动的高斯网变形效果。每种物体第一行依次展示了待变形的网格和数据驱动变形后的网格，第二行展示了变形前的渲染图片和数据驱动变形后的新视角合成图片。从图示结果可以看出，用户可以通过编辑控制顶点来实现高真实感高度的变形建模。

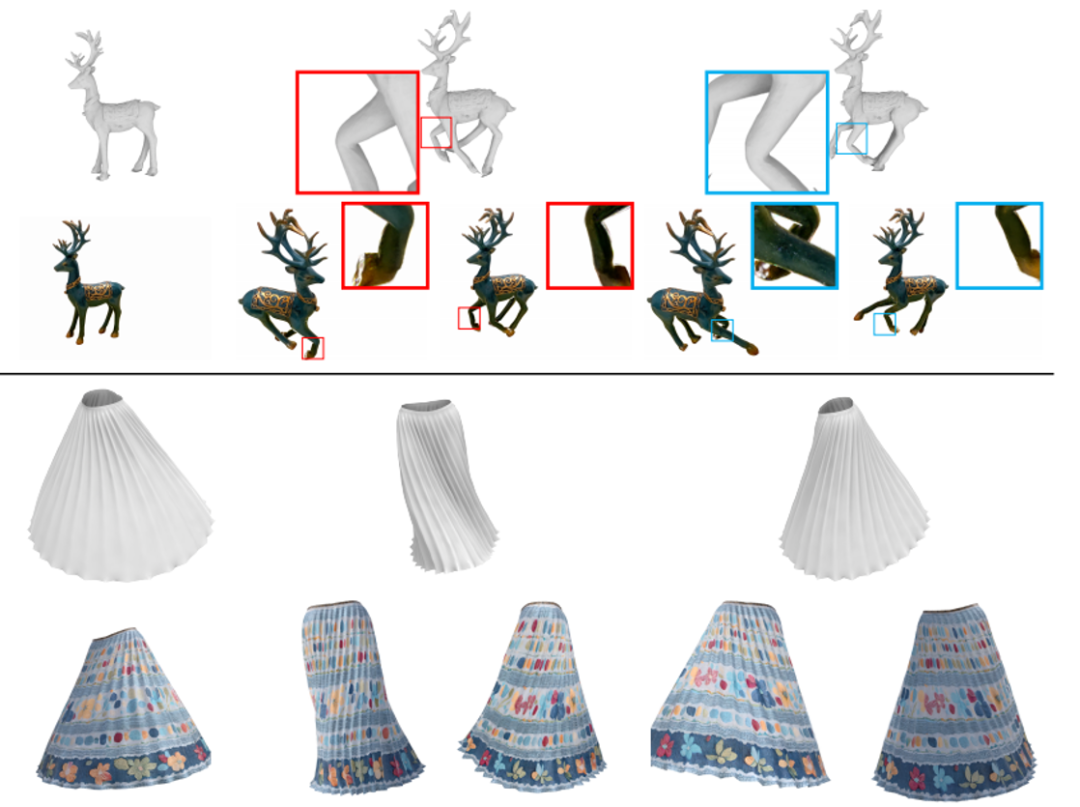
图11 基于数据驱动变形方法的高斯网变形[2][3]，用少量交互实现了具有复杂运动的变形

计图开源

https://github.com/IGLICT/GaussianMesh

项目的主页为: 

http://www.geometrylearning.com/GaussianMesh/

计图(Jittor)是清华大学开源的自主深度学习框架，完全基于动态编译，采用元算子融合和统一计算图的新技术，并支持国产硬件。元算子易于使用，便于算子的开发和优化，而统一计算图则是融合了静态计算图和动态计算图的诸多优点，在易于使用的同时提供高性能的优化。计图官网为：

https://cg.cs.tsinghua.edu.cn/jittor/

1. Lin Gao*, Jie Yang, Bo-Tao Zhang, Jia-Mu Sun, Yu-Jie Yuan, Hongbo Fu, and Yu-Kun Lai: Real-time Large-scale Deformation of Gaussian Splatting. ACM Transactions on Graphics, 2024, 43(6):1-16. 

2. Lin Gao*, Yu-Kun Lai, Jie Yang, Ling-Xiao Zhang, Shihong Xia, Leif Kobbelt: Sparse Data Driven Mesh Deformation. IEEE Transactions on Visualization and Computer Graphics, 2021, 27(3), 2085-2100. 

3. Lin Gao, Yu-Kun Lai, Dun Liang, Shu-Yu Chen, Shihong Xia: Efficient and Flexible Deformation Representation for Data-Driven Surface Modeling. ACM Transactions on Graphics, 2016, 35(5), 158:1-158:17. 

4. Yu-Jie Yuan, Yang-Tian Sun, Yu-Kun Lai, Yuewen Ma, Rongfei Jia, and Lin Gao: Interactive NeRF Geometry Editing With Shape Priors. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2023, 45(12): 14821-14837.

5. Shi-Min Hu, Zheng-Ning Liu, Meng-Hao Guo, Jun-Xiong Cai, Jiahui Huang, Tai-Jiang Mu, Ralph R. Martin: Subdivision-Based Mesh Convolution Networks. ACM Transactions on Graphics, 2022, 41(3), 25:1-25:16.

6. Guédon A, Lepetit V. Sugar: Surface-aligned gaussian splatting for efficient 3d mesh reconstruction and high-quality mesh rendering, CVPR 2024, 5354-5363

7. Joanna Waczyńska, Piotr Borycki, Sławomir Tadeja, Jacek Tabor, Przemysław Spurek: Games: Mesh-based adapting and modification of gaussian splatting. arXiv preprint arXiv:2402.01459, 2024.

8. Bernhard Kerbl, Georgios Kopanas, Thomas Leimkühler, George Drettakis: 3D Gaussian Splatting for Real-Time Radiance Field Rendering. ACM Transactions on Graphics, 2023, 42(4), 139:1-139:14.

9. Charles Loop: Smooth Subdivision Surfaces Based on Triangles. Masters Thesis, Department of Mathematics, University of Utah, 1987.

GGC往期回顾