计图开源：基于不变性的无监督三维模型对称性分析

2023/09/16 Tutorial

计图开源：基于不变性的无监督三维模型对称性分析

对称性是三维模型的一种重要属性，可以用于三维重建、姿态估计和形状匹配等重要任务。近期，中科院计算所研究团队和英国卡迪夫大学研究人员合作，提出了一种新的无监督的三维模型对称性检测方法E3Sym[1]，该方法利用E(3)不变特征建立鲁棒的点对应关系来提取对称平面，无需人工标注数据，通过自监督的方式即可高效准确地分析三维模型的镜面对称性，并且该方法能够有效处理不完整模型和具有任意数量对称平面的三维模型。该论文已被ICCV 2023录用。

图 1 E3Sym对称平面检测结果

Part 1

问题和背景

对称性是自然界中无处不在的现象，在过去的几十年里，对称性检测在二维和三维上都受到了广泛的关注。作为三维形状的一个重要属性，对称性可以应用于多种任务。在E3Sym中，研究人员聚焦在检测三维形状的全局反射对称性。

早期的进展大致可以分为三类：基于匹配的方法、基于采样的方法和基于回归的方法：
  • 基于匹配的方法通过匹配局部形状特征来检测对称性，生成潜在的对称平面，并进行优化以得到合理的解决方案。因此，基于匹配的方法的关键是使局部形状特征具有鲁棒性或不变性，以应对欧氏变换。
  • 基于采样的方法通过在变换空间中大量采样并进行进一步验证来检测对称性，这一类方法主要面对的问题是：如果进行穷举采样则会引入高计算复杂度，如果进行启发式采样会引入不准确的候选对称性并且需要更加复杂的优化步骤。
  • 基于回归的方法借助深度神经网络的表达能力和大量训练数据，通过有监督或无监督的方式来回归对称参数或对称点坐标，以达到检测对称性的目的。

PRS-Net [2]是第一种无监督的对称性检测方法，可以同时检测反射和旋转对称性，然而，该方法限制了预测的反射平面和旋转轴的数量，并且随着预测的反射平面和旋转轴数量的增加，网络参数也近似线性增加。

如果我们能够从三维模型中建立准确的对称性对应关系，依据对应关系对称平面就可以计算得到了。一般来说，具有相似外观或几何结构的对称对应关系是位置和方向不变的。对应关系匹配是基于这样一个事实：对称点之间的局部几何模式是不变的，并且不应该受到对称变换的影响。尽管这看起来很直观，但如何准确而鲁棒地建立对应关系仍然是一个挑战，这也是基于匹配的方法主要面临的问题。进一步来讲，当形状是不完整的时候，检测对称性就更加困难了。

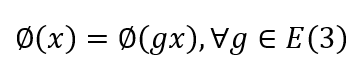
在该文中，研究人员提出了一种新颖的检测三维全局反射对称性的方法E3Sym。E3Sym通过使用一个轻量级的神经网络提取局部区域的E(3)不变特征（这些特征在任意欧氏变换下都保持不变）来建立鲁棒的点对应关系，从而得到稠密的对称平面预测结果，之后引入了一种新颖而高效的对称平面聚合算法得到最终的对称平面。值得注意的是，E3Sym不仅具有从不完整形状中检测全局反射对称性的能力，而且能够处理拥有任意数量对称平面的三维模型。
注：上述提到函数具有E(3)不变性，是指对于任意的三维空间中的欧式变换g，满足：

E(3)群是三维欧式空间的对称群，包含三维空间中的所有平移、旋转和反射变换，以及它们的任意有限组合。

Part2
方法概述
如图2所示，E3Sym首先提取点云中每个点的局部邻域，通过提取局部邻域的E(3)不变特征作为该点的几何特征，利用可微分的DiffTopK方法在特征空间中建立点和点之间的对应关系，得到稠密的对称平面，最后通过新颖而高效的对称平面聚合算法SymGroup，产生最终的对称平面检测结果。为了实现无监督训练，该方法使用和PRS-Net[2]一样的对称距离损失函数来优化网络。

图 2 E3Sym方法概览

具体而言，如图3所示，E3Sym首先借助Frame Averaging [3]，使得PointNet结构的点云特征提取网络φ对E(3)不变，进而得到逐点的E(3)不变特征，这也是后续特征匹配和稠密对称平面检测的前提。

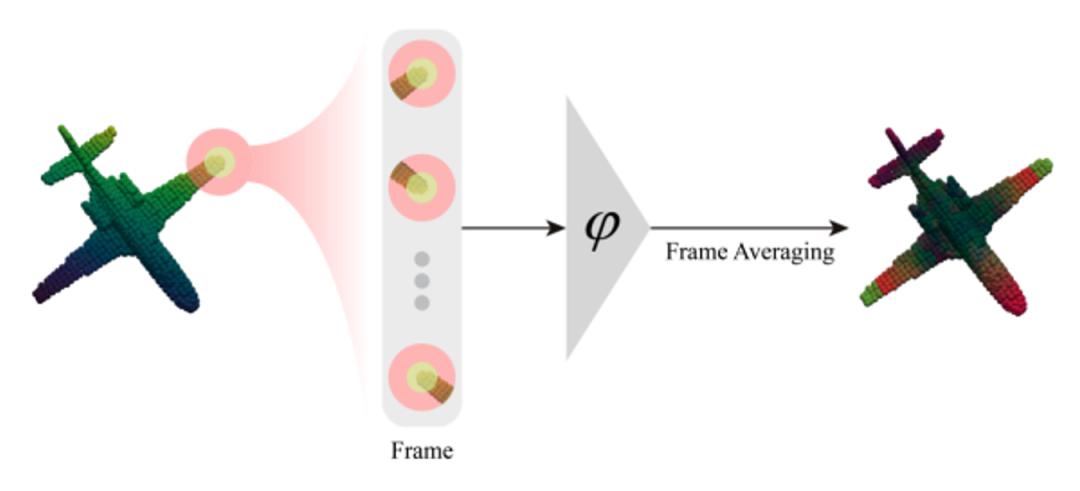
图 3 E(3)不变特征提取

在得到稠密对称平面之后，如图4所示，E3Sym通过提出的对称平面聚合算法SymGroup得到最终的对称平面检测结果。具体地说，SymGroup首先建立一个无向有权图，其中顶点由稠密对称平面组成，如果两个平面距离足够近，那么对两个顶点之间赋予一条边，权重与其之间的距离成负相关，接着在该无向有权图中寻找联通分量，并取联通分量的中心作为最终的对称平面检测结果。

图 4 SymGroup算法流程示意图

Part 3 

结果展示
如图5所示，E3Sym能够准确处理拥有任意数量对称性的三维模型，而PRS-Net[2]只能预测3个对称平面，展示了E3Sym准确处理具有任意数量对称平面的三维模型的能力。

图 5 不同方法对称平面检测可视化结果

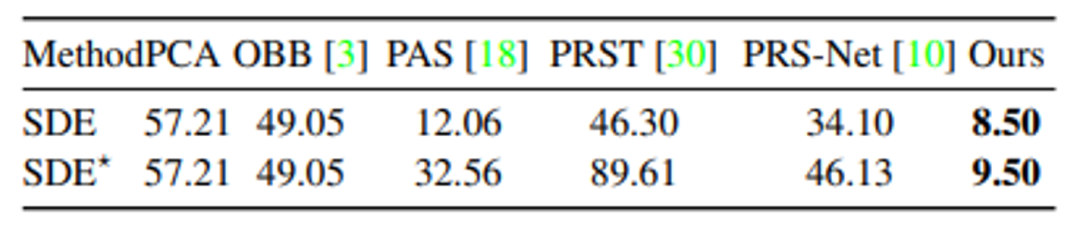
E3Sym在三维模型数据集ShapeNet上进行了评测，使用对称距离误差（SDE）和F-Score作为评测指标，如表1所示，E3Sym在两项评测指标上均显著优于基准方法。

表 1 不同方法在ShapeNet测试集上的对称距离误差（SDE）和F-Score对比

为了验证E3Sym在不完整形状上的鲁棒性，研究人员分别在Partial ShapeNet和MVP数据集上验证了不同算法的表现，数值结果分别如表2和表3所示，可以看到，E3Sym均取得了更优的性能。

表 2 不同方法在Partial ShapeNet上的SDE对比结果

表 3 不同方法在MVP上的SDE对比结果

可视化案例如图6所示，对MVP数据集中的不完整形状来说，E3Sym仍然能得到合理的结果。

图 6 在MVP数据集中不同三维模型的对称平面检测可视化结果

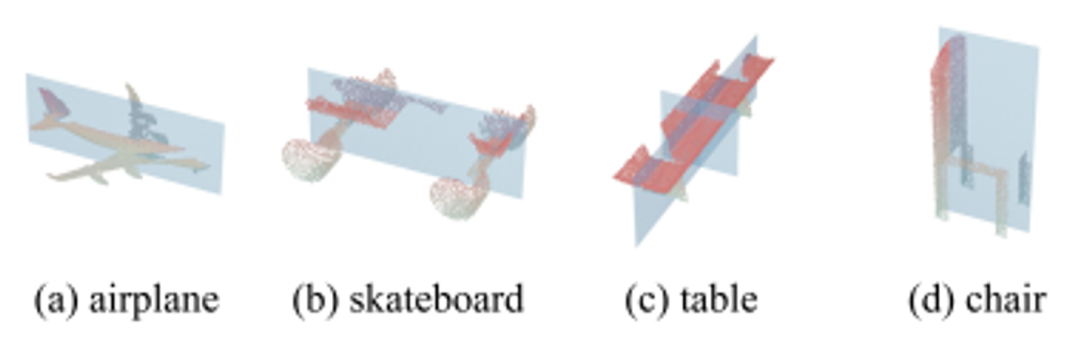
图7展示了E3Sym通过反射对称性推理旋转对称性的示例，对于八面体和一些典型的具有旋转对称性的物体，E3Sym均能正确推理出来。

图 7 旋转对称性推理
图8展示了E3Sym在形状补全上的应用，得益于准确的对称性检测，补全的形状在几何上更加准确，完整度更高，并且在Chamfer Distance上取得更好的数值。

图 8 不同方法形状补全对比 ，数值代表Chamfer Distance

Part 4

结语
E3Sym是一种端到端的、无需任何标注数据的无监督三维全局反射对称性检测方法，其核心思想是首先通过E(3)不变特征来鲁棒地建立稠密的、逐点粒度的对称性对应关系，然后使用可微的聚类方法得到最终的全局对称平面检测结果，并且可处理不完整模型和具有任意数量对称平面的模型。
在未来，如何将其扩展到旋转对称性和内蕴对称性检测上值得继续研究，同时鉴于全局镜面对称性作为三维模型的重要属性之一，这项技术将在几何建模、三维重建等应用中发挥作用。
目前E3Sym基于计图(Jittor)实现的代码已经在github开源：
https://github.com/renwuli/je3sym
计图实现的代码相比Pytorch代码在相同参数与配置下，显存占用减小了50%。

参考文献

  1. Ren-Wu Li, Ling-Xiao Zhang, Chun-Peng Li, Yu-Kun Lai and Lin Gao, E3Sym: Leveraging E(3) invariance for unsupervised 3D planar reflective symmetry detection, ICCV, 2023
  2. Lin Gao, Ling-Xiao Zhang, Hsien-Yu Meng, Yi-Hui Ren, Yu-Kun Lai, and Leif Kobbelt, PRS-Net: Planar reflective symmetry detection net for 3D models，IEEE TVCG, 2021
  3. Omri Puny, Matan Atzmon, Heli Ben-Hamu, Edward J Smith, Ishan Misra, Aditya Grover, and Yaron Lipman, Frame averaging for invariant and equivariant network design，ICLR, 2022

GGC往期回顾

1. CVM 2024 征文四周后截稿，欢迎大家踊跃投稿、相聚新西兰！

2. 视觉骨干网络VAN | CVMJ Spotlight

3. Computational Visual Media第9卷第4期导读

4. CVMJ获最新期刊影响因子6.9，计算机图形学领域排名第一

5. 计图全面支持大模型的训练和推理，发布可在线测试的开源应用案例

您可通过下方二维码，关注清华大学计算机系图形学实验室，了解计算机图形学、Jittor深度学习框架、CVMJ期刊及CVM会议的相关资讯。

Search

    Table of Contents