对称性是三维模型的基本属性之一。通过分析三维模型的对称性，有助于诸如模型识别、分析、补全等任务。近期，马里兰大学、中科院计算所、中国科学技术大学和英国卡迪夫大学的学者合作，在IEEE TVCG合作发表一项关于网格内蕴对称性检测的成果[1]。该工作提出了一种基于学习的三维模型内蕴反射对称性的检测方法，提高了检测的速度、精度和鲁棒性，并开源了基于计图(Jittor)框架实现的代码。

Part1

研究背景

在模型对称性的研究领域，研究人员主要关注空域中的外蕴(extrinsic)对称性和内蕴(intrinsic)对称性。外蕴对称性定义在欧式空间中，指刚性变换(包含反射变换)下形状的不变性，大家熟知的镜面对称、旋转对称即属于此类。内蕴对称性定义在非欧(流形)空间中，指自同胚映射下流形形状的不变性(即各点之间测地距离不变)。形式化的说，若流形O上存在一个同胚映射T对流形上任意两点p和q保持测地距离，即满足以下公式：

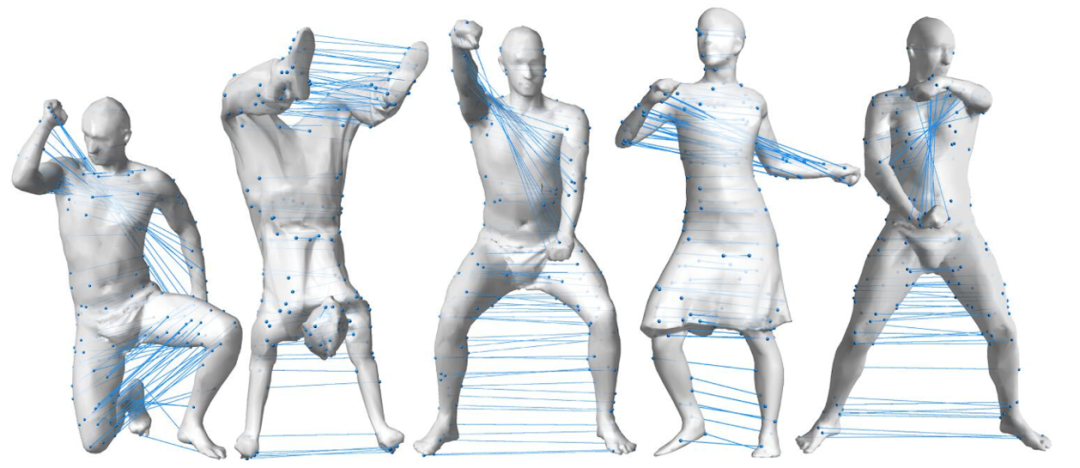
则称O是内蕴对称的。其中g(p,q)表示流形上点p和点q的测地距离。图1展示了该研究工作对于人体的内蕴对称性的检测结果，映射前后的对应点用蓝线相连。

图1：人体内蕴对称性的检测结果

之前的研究工作往往依赖于采样和投票，会产生较大的计算开销，并且结果不够鲁棒。该工作提出了几何深度学习的方式来进行内蕴对称性的检测，比以往工作的推理速度提升了20倍以上。

Part2

方法概述

最为直接的描述内蕴对称变换T的方式是在模型上表示对称点之间的两两对应，然而这个对应矩阵会有很高的维度，且难以在此表示之上进行进一步的优化。为此，该工作使用functional map[2]来表示要估计的内蕴对称变换。在该表示下，流形到流形之间的变换可以等价转化为其对偶函数空间上的变换。该方法选用拉普拉斯－贝尔特拉米算子的特征函数作为此函数空间的基底函数，即可将这个函数空间的变换，进一步转变为在此函数基底所定义的坐标上的映射，这一映射矩阵记为C。

特别地，由于拉普拉斯－贝尔特拉米算子是在等距变换下的不变量，其特征子空间在内蕴对称变换下亦保持不变，子空间里的函数在变换下都会映射回子空间内部，故内蕴对称变换的矩阵应该为分块对角矩阵。对于有非重复特征值的特征函数（即子空间只有一个函数），对应的特征函数Φ在（等距）对称变换下只有以下两种情况[3]:

相应的矩阵C对角线上第i的元素分别取值+1与-1。于是，内蕴对称性检测的问题归结为对于特征函数的符号的判断。图2展示了不同三维模型上的特征函数，其中第一行是正特征函数，第二行是负特征函数，可见正特征函数是对称的，而负特征函数是反对称的。

图2：拉普拉斯－贝尔特拉米算子特征函数的可视化

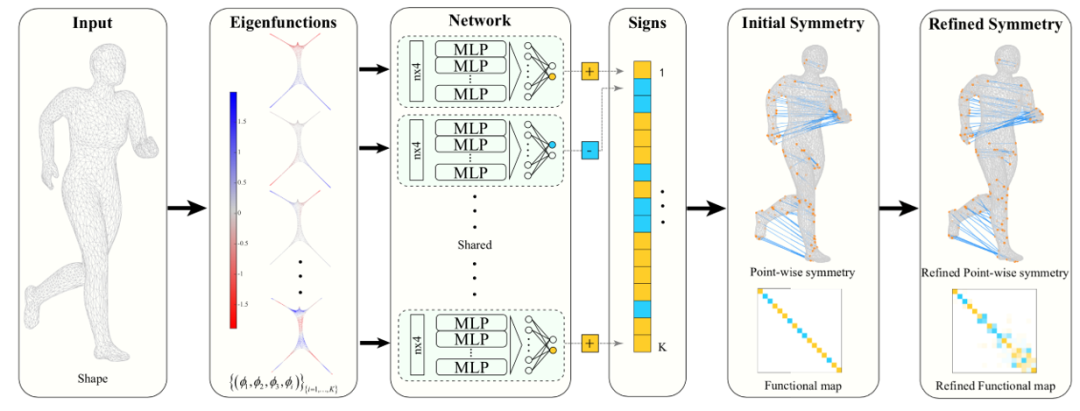
如图3所述，该工作首先对输入的二维流形计算前K个特征函数，通过提出的基于MLP的神经网络SignNet预测这些特征函数的符号，将这些预测的值转化成函数空间的映射矩阵，从而得到对于对称性的初始预测。经过神经网络预测对角线值之后，该方法进一步通过后处理步骤对初始预测进行修正，这一步后处理同时也解决了对于有超过一个特征函数的特征子空间（重复特征值），即映射矩阵C在对角线之外也有非零值的情况。SignNet在预测第i个特征函数φi的符号时，将前t个(在该方法中取t=3)特征函数和φi一同输入网络中，而不输入例如坐标等在等距变换下有变化的特征。这样的输入可以内蕴地对输入的网格特征进行表示，避免了同一模型的不同变形带来的影响。

对于SignNet预测得到的初始映射矩阵，还需要进行一步后处理。如前文所说，实际的网格模型其实并不是完美内蕴对称，其上也会有一维以上的特征子空间，这些都会导致特征函数在模型上的分布不是绝对的内蕴对称/反对称。为了微调这些分布得不好的特征函数，该工作选择迭代优化一个正交的矩阵，使得这些特征函数在线性映射下保持对称。优化的目标包括保持特征值矩阵的性质和使得模型上的点在两次对称变换后能映射回它自身。

图3：本研究工作的算法示意图

Part3

结果展示

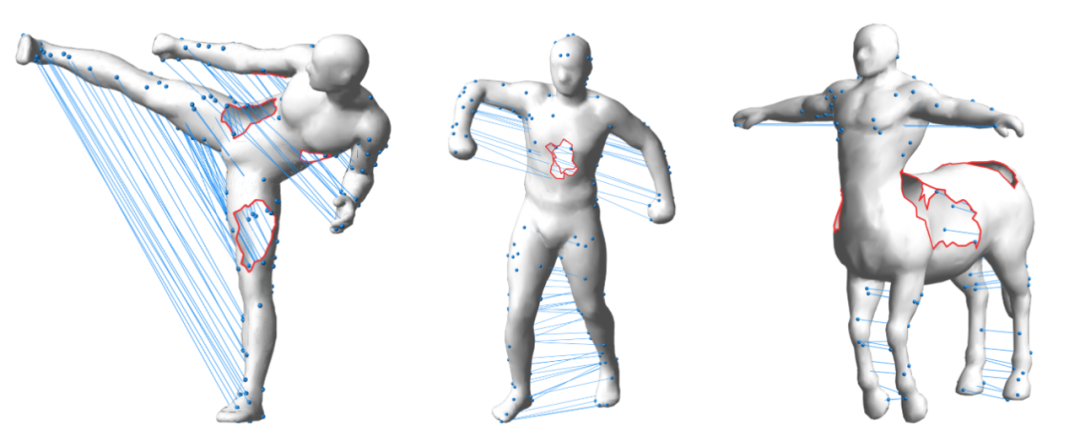
该工作相比以往工作检测速度有超过20倍的提升。同时对应比例(correspondence rate)和成功预测比例(mesh rate)也超过了以往的工作。如下表格展示了SCAPE数据集上的比较结果：

该工作在不同的形状上展示出了良好的泛化性能，并且对于残缺网格的内蕴对称性检测有较好的鲁棒性。如图4、图5所示：

图4：不同形状上的内蕴对称性检测结果

图5：在残缺网格上的内蕴对称性检测结果

Part4

计图开源、训练与推理均大幅提升

该项研究工作已经发表于CCF A类期刊IEEE TVCG上，并在图形学知名会议CVM 2022上进行了报告。该论文作者包括美国马里兰大学的博士生乔怿凌、中国科学院的陈熙霖研究员、高林副研究员和硕士生刘树智，英国卡迪夫大学的来煜坤教授和中国科学技术大学的刘利刚教授。

目前该工作已经发布基于计图(Jittor)的开源代码：

https://github.com/IGLICT/intrinsicSym-Jittor

基于计图实现的代码训练速度是Tensorflow版本的1.57倍，推理速度是Tensorflow版本的1.53倍。

参考文献

1. Yi-Ling Qiao, Lin Gao, Shu-Zhi Liu, Ligang Liu, Yu-Kun Lai, Xilin Chen, Learning-based Intrinsic Reflectional Symmetry Detection, IEEE Transactions on Visualization and Computer Graphics, 2022, doi: 1-10,10.1109/TVCG.2022.3172361

2. Maks Ovsjanikov, Mirela Ben-Chen, Justin Solomon, Adrian Butscher, Leonidas Guibas, Functional Maps: a Flexible Representation of Maps between Shapes, ACM Transactions on Graphics, 2012, Vol. 31, No. 4, 30:1-30:11.

3. Rajendra Nagar, Shanmuganathan Raman, Fast and Accurate Intrinsic Symmetry Detection, ECCV, 2018, 417–434.

GGC往期回顾

1. 平面四边形网格自支撑曲面的构造 | CVMJ Spotlight

2. 计图开源：高林团队CVPR发文, 提出基于NeRF的场景风格化方法

3. 斯坦福图形学教授Leonidas J. Guibas当选美国科学院院士

4. 计图开源：清华刘玉身团队发表PAMI论文，提出点云补全网络PMP-Net++

5. 第二届“计图”人工智能算法挑战赛启动

您可通过下方二维码，关注清华大学计算机系图形学实验室，了解计算机图形学、Jittor框架、CVMJ期刊及会议的相关资讯。