近日，清华大学计算机系图形学实验室和斯坦福大学、英伟达公司合作，提出Synorim多点云非刚性注册方法，利用可学习基函数所导出的“函数式映射”（Functional Maps）来描述点云之间的匹配关系，并运用函数式同步来恢复特征的典范空间，增强多输入点云的循环一致性。该工作已经被IEEE T-PAMI录用。

Part 1

研究背景

近年来随着三维传感器的普及，大量的三维数据被广泛应用于影视采集、动画、机器人等领域，并正在逐步革新传统的二维计算机视觉。而在诸多应用中，需要从多个视角长时间采集柔性的运动物体，例如运动的人、动物、布料等。这就需要一个有效的算法，将不同视角、不同时间的三维信息进行对齐，建立三维匹配关系，从而为后续的重建、属性迁移或特征融合等任务提供坚实基础。

然而，上述任务存在着三点主要的挑战：1) 从传感器获取到的三维数据通常以点云（三维点的无序集合）进行表示，点云之间缺失拓扑连接关系，难以约束变形场；2) 点云数据通常存在视角的（自）遮挡、噪声，为匹配带来较大歧义性；3) 对于多帧动态点云缺乏有效的匹配一致性约束手段进行多输入的闭环。

 

图1 本方法的各个步骤图示

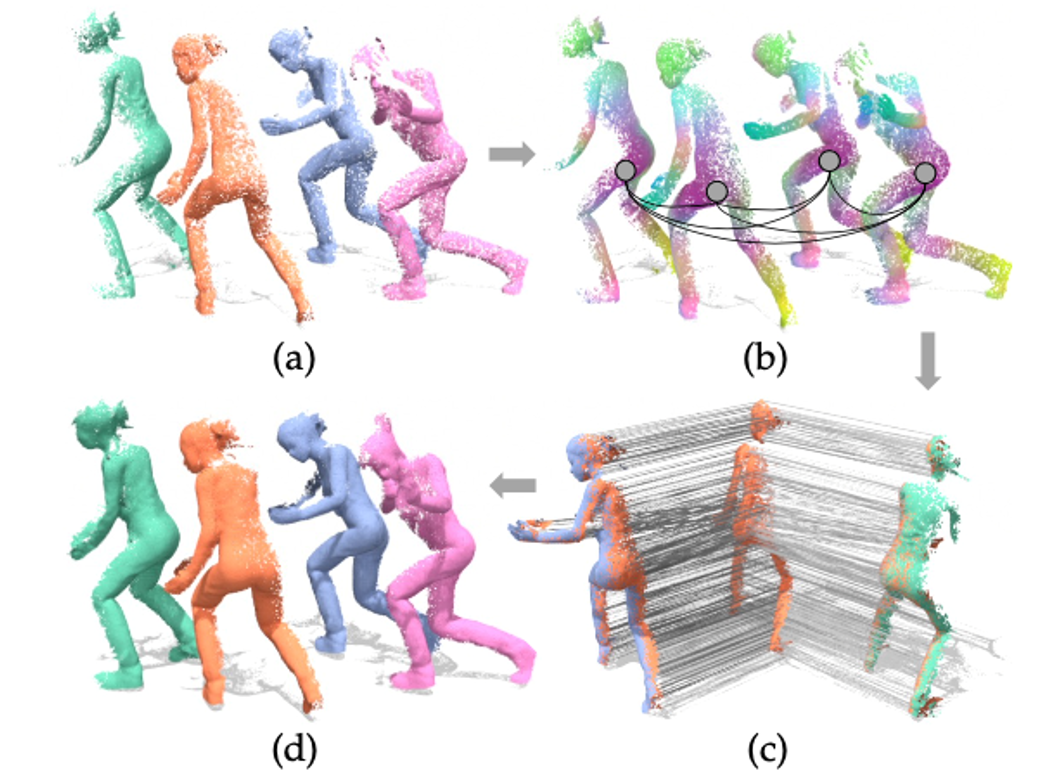
清华大学计算机系图形学实验室的这一工作对上述的挑战进行了有益的尝试，在4个典型数据集上取得领先性能，并在FAUST在线挑战的自动化方法中排名第二。图1给出了本方法的各个步骤，其中，a）为输入点云，b）为特征典范空间， c）为帧间场景流，d）为最终注册结果。

Part 2

多视角点云的联合注册

问题定义

• 输入：多帧点云{X_1,…,X_K}，每个点云被表示为Nx3的张量；

• 输出：从任意源点云X_k到任意目标点云X_l的三维场景流F_{kl}，该场景流与源点云坐标相加X_k+F_{kl}之后，能够将源点云变形到与目标点云一致的形状。

函数式映射

由于点云的柔性变换并非任意，一般具有运动连续性，即大部分相邻的点运动差距不会过大，因此通过使用有限个数的基函数来对点云进行刻画，从而适配这种低秩（Low-rank）的特性。

这样一来，点云之间的稠密映射与对齐关系就可以转换为少量“定义在点云上的函数”之间的映射关系——后者不仅能为柔性注册提供较好的低秩归纳偏置，也能有效提高算法效率。函数式映射的另一个优势在于其线性性，在离散情况下即可以通过一个小型的矩阵Ckl（如24x24）表示，允许使用线性代数工具进行求解。

可学习基函数

传统的函数式映射已经被部分用在图形学中的形状匹配中，通过网格表达的显式拓扑关系能够导出形状的内蕴矩阵，并能够谱分解出由粗到细的特征基函数。而对于不存在拓扑关系的点云，前人一般采用基于kNN或Delaunay三角化等方法建立连接关系，本方法则通过深度学习的方式来为每个点云X_k预测出一组基函数φ_k。本方法没有显式约束基函数的正交性，为了将任意函数投影到基函数上获得其函数坐标，作者采用了基于SVD的伪逆技术来获取函数坐标的闭式解。

场景流计算

在为每个点云计算了基函数之后，可通过另一个小型的匹配网络计算点云对的稀疏匹配关系，由于遮挡、柔性变形等因素该匹配将存在噪声。为了获取平滑的稠密匹配，即场景流F_{kl}，可以先根据稀疏匹配计算函数式映射矩阵，即求解如下能量函数的最小参数值问题：

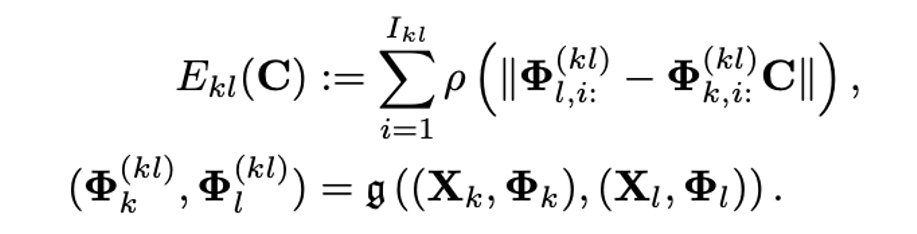
在上述方程中，为了进行函数映射，只需要将函数式映射矩阵C右乘到基函数上即可。作者还使用鲁棒核函数ρ进行逐项加权来减弱噪声影响。该能量函数最小参数值问题可以使用IRLS方式求解，并采用迭代展开的方式获取梯度进行端对端训练。

为了计算场景流，该论文研判了如下两种方式，第一种方式通过计算函数映射完成之后的基函数高维特征距离来确定点云一对一软匹配：

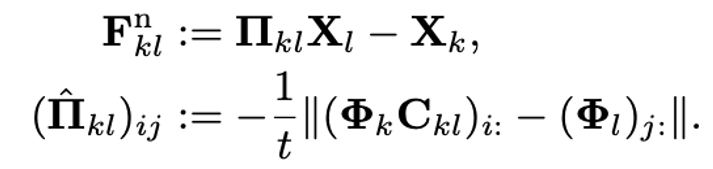
这种方式较为精确，但不能处理遮挡问题，映射空间受限于目标点云凸包内部；第二种方式则通过求取映射目标点云“坐标函数”的函数坐标进行直接映射：

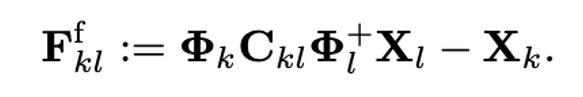
这种方式能够优雅地处理遮挡，但是由于基函数的个数限制抹去了点云坐标本身的高频几何细节，注册精度将有所下降。因此，最终的场景流预测通过端对端学习的方式结合了上述两种不同计算方式，取得了最优的效果。本方法的整体训练流程如图2所示。

图2 本方法训练流程

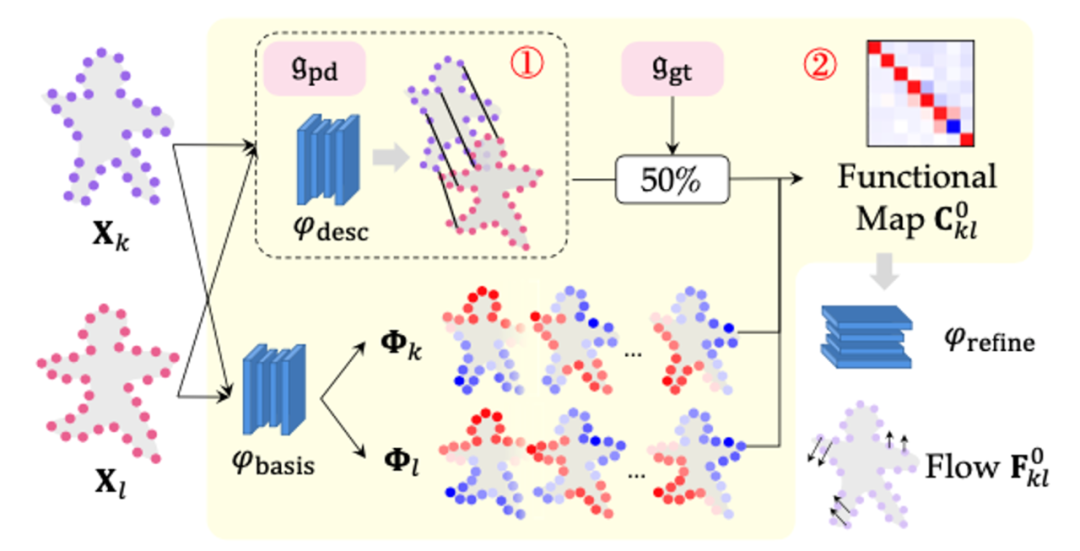
函数式同步

上述方法能够完整计算出每个点云对的柔性注册情况。对于多输入的点云，在推理阶段，可额外引入了函数式同步方案来利用多视角信息，如图3所示。

图3 推理阶段有多输入点云时的方法示意

直观上来讲，同步所追求的循环一致性就是强调：若点A与点B匹配，点B与点C匹配，则A与C的匹配概率将大大提升。在考虑到这种特性下的联合建模能够有效通过几何一致性提升匹配准确度。而本方法则利用上述步骤中求取的函数式映射关系，在“函数空间”（而非点云级别的匹配空间）中进行一致性约束。

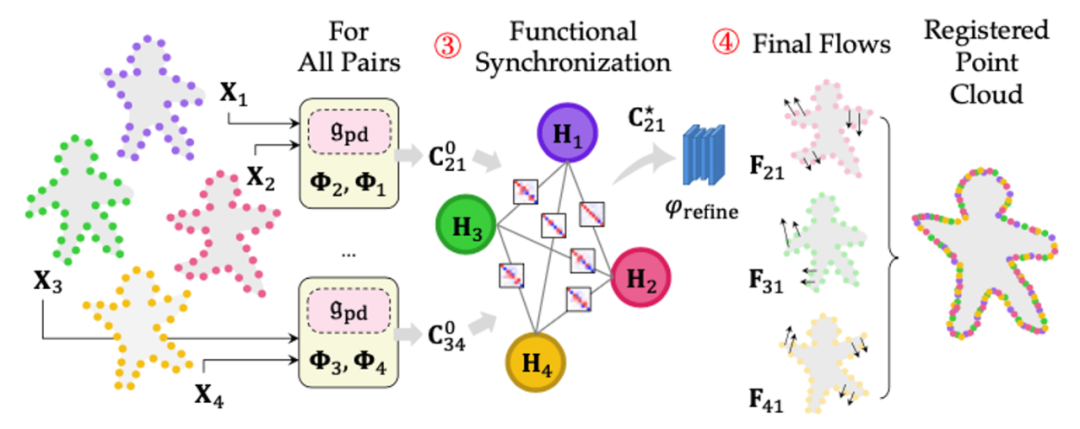
具体来说，作者将求解优化之后的新函数映射矩阵，以及一个函数坐标的典范空间H_k。该典范空间描述了一组函数（以基函数下的坐标表示），使得通过链式的函数矩阵C_{kl}映射之后，映射结果能够保持路径无关的特性：

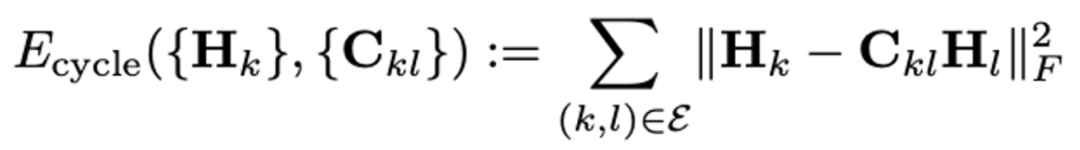
作者采用的优化算法交替式对典范空间H_k和函数映射矩阵C_{kl}进行优化，使得上述能量函数与E_{kl}(C)的求和尽可能小。在计算完成之后，就可将优化后的函数映射矩阵带入场景流计算模块，求得优化更新后的场景流。受益于多点云的输入，由具有循环一致性的函数导出的匹配关系精度能够进一步提升。

Part 3

实验结果

该论文在4个典型数据集上进行了实验，分别为CAPE人体扫描数据集、DeformingThings4D柔性体合成数据集(包括类人与动物)、DeepDeform深度相机扫描数据集、以及SAPIEN多刚体数据集。与基线方法的对比中，该方法都取得了最优的注册精度。相关的定性与定量结果如表1、图4、图5所示。

表1 CAPE数据集在全监督和自监督设定下的精度和时间对比 

图4 DeformingThings4D数据集定性效果比较 

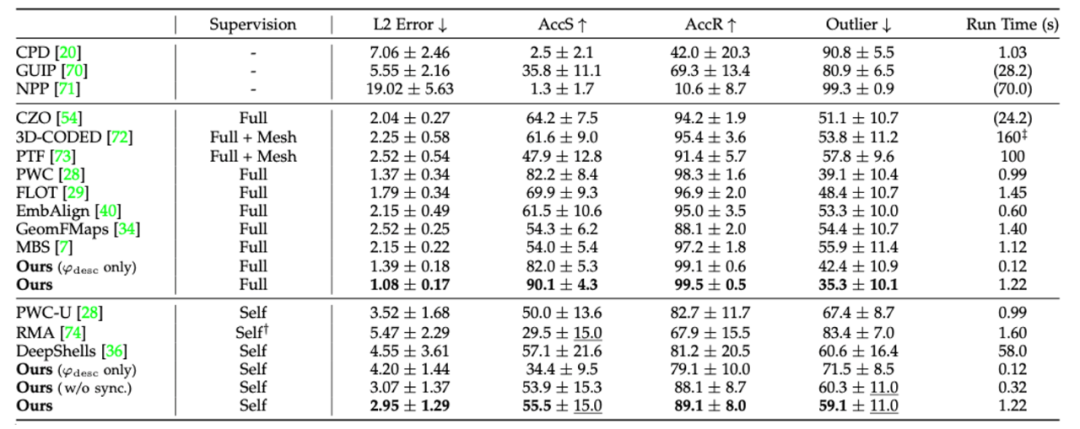
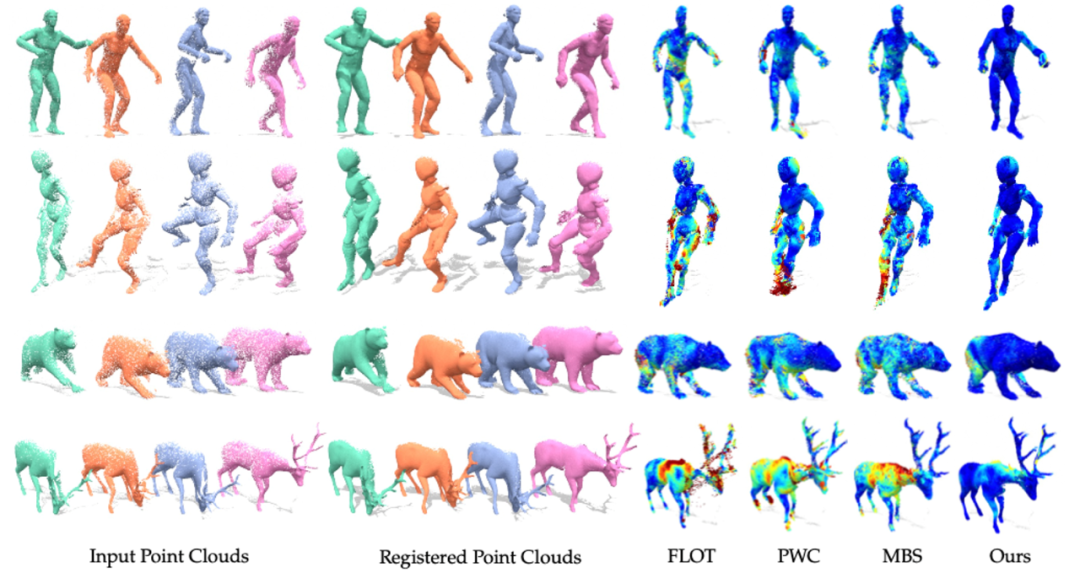
图5 SAPIEN数据集定性效果比较

在FAUST在线挑战中（测试集真值未知），该方法也在所有的自动化方法中取得了第二的成绩，但速度更快、泛用性更强；如表2所示。

表2 FAUST挑战定量结果 

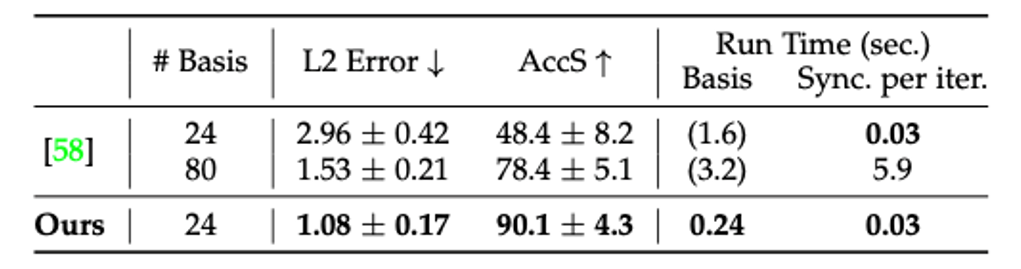
为了证明可学习基函数的有效性，作者将该方法与传统几何方法[58]进行了对比，在只使用24个基函数的情况下，可学习基函数的性能即可远超传统方法使用80个基函数的性能。

表3 不同的基函数性能对比 

多帧同步之后的点云能够有效实现闭环，并支持稀疏视角的动态三维重建，效果如图6所示。

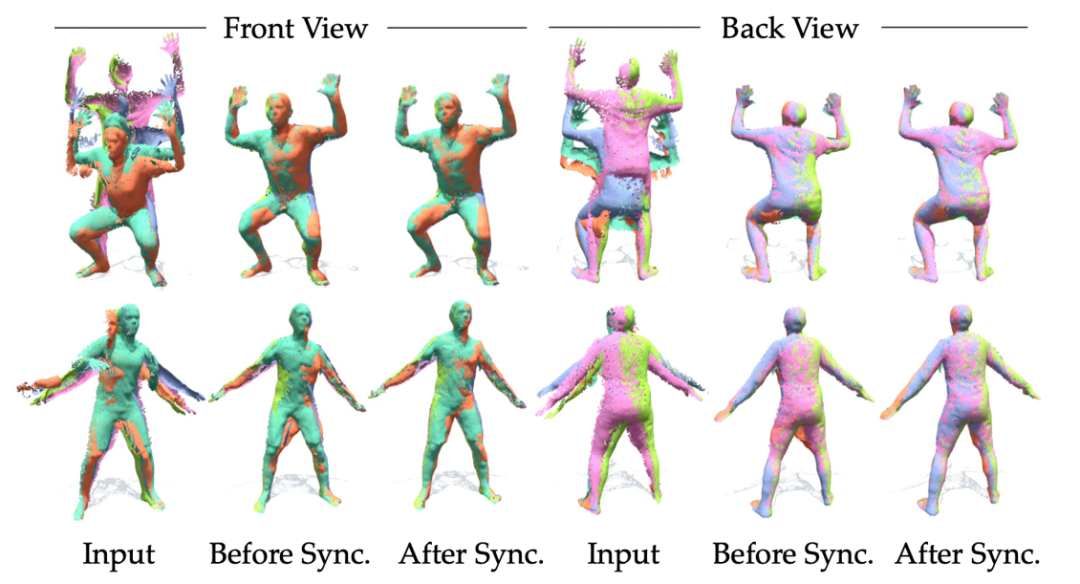
图6 本方法的动态闭环与稀疏视角重建示意

Part 4

总结

本方法能够有效对齐缺失、噪声下多视角点云，并从点云注册的内部机理出发，提供了一种有益的描述柔性体运动的函数式表示形式，使得在这种表示下多帧一致性与精度能够得到有效增强。

然而，本方法也存在问题，诸如：大型形变下运动欠拟合、跨越不同类型泛化性欠佳等，欢迎后续的研究者共同参与讨论，为本方案提出宝贵意见。该论文的代码已经基于计图(Jittor)框架开源，详见论文的项目主页和Github仓库。

项目主页：

https://cg.cs.tsinghua.edu.cn/project/synorim/

Jittorkai开源：

https://github.com/heiwang1997/synorim-jittor

参考文献

1. Jiahui Huang, Tolga Birdal, Zan Gojcic, Leonidas J Guibas and Shi-Min Hu, Multiway Non-rigid Point Cloud Registration via Learned Functional Map Synchronization, arXiv preprint arXiv:2111.12878, 2021.

GGC往期回顾

1. 计图开源: 图匹配网络SuperGlue的优化！速度超TensorRT、显存省一半以上

2. CVMJ刊发视觉注意力机制综述，Github 仓库获star1400+

3. Jittor团队提出大核注意力，开源新的骨干网络VAN

4. 第十届CVM会议4月在北京举行，会议议程发布了！

5. 首届JDC召开，计图技术委员会评出2021年度优秀Jittor开源项目

您可通过下方二维码，关注清华大学计算机系图形学实验室，了解计算机图形学、Jittor框架、CVMJ期刊及会议的相关资讯。