对称性是三维模型的重要属性之一，对三维模型进行对称性分析，可以用于几何模型识别、分析和建模等任务。中科院计算所在计算机图形学顶级期刊IEEE TVCG上发文，提出了一种无监督的三维模型对称性分析方法PRS-NET，该方法利用了对称模型本身具有的对称性的特性，无需人工标注的数据就可以对深度网络进行训练，从而可以高效准确的分析三维模型的对称性属性。

该项目研究团队包括中科院计算所的高林副教授和张凌霄、英国卡迪夫大学的Yu-Kun Lai教授和德国亚琛工业大学的Leif Kobbelt教授等。

下图先展示一下PRS-NET在ShapeNet数据集上部分模型的对称平面检测结果。

图1 PRS-NET对称平面检测结果

经典的研究工作基本步骤是首先在模型表面随机采样，计算特征并在特征空间进行聚类，进而提取对称信息[1,2,3]。近年来，随着深度学习技术的发展，有监督的方法被提出用于分析三维模型的属性包括对称性。PRS-NET[4]利用对称模型的特性，提出了度量对称程度的可微损失函数，实现了无监督的网络训练过程，相比经典方法，计算速度更快，鲁棒性和精度更高。

Part1

PRS-NET方法概述

由于大部分人造模型基本只有三个以内的对称平面，剩下的一部分为扫描体模型，如花瓶、易拉罐等，所以网络设计输出三个对称平面已经足够表示大部分人造模型的全局对称性，对于少部分扫描体模型，使用对称平面并不能很好的表示其对称性，也无法直接通过预测的对称平面来判断一个模型是否是扫描体，因此，同时设计了网络输出三个旋转对称的参数，得到对应的旋转轴来表示扫描体的全局对称性（见图2）。

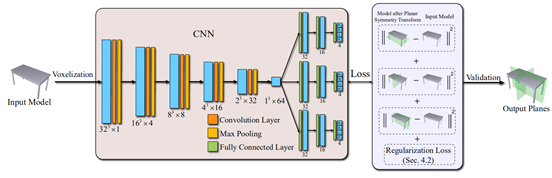
图2 PRS-NET无监督对称性分析方法的网络结构设计

为了实现无监督的训练，作者提出了新颖的对称距离损失函数来优化网络，同时为了避免网络输出重合的对称平面与旋转轴，还加入了正则项约束。

对称距离损失函数衡量模型在给定平面下的对称程度，计算模型表面采样点相对给定平面的对称点到模型的距离。该距离的大小衡量了给定平面的对称程度，且计算过程是可导的，从而实现了对网络的无监督训练。具体定义详见论文。

Part2

结果展示

PRS-NET在三维模型数据集ShapeNet, ABC以及Thingi10K上面进行了数值对比，为了能更好的比较不同方法的优劣，作者标注了ShapeNet上的部分测试集模型的对称平面参数，用来对比不同方法检测的平面与标注结果的差距，数值结果比较如图3，图4所示。

图3 不同方法在ShapeNet测试集上真值误差(GTE)以及对称距离误差(SDE)对比

图4 不同方法在ABC 以及 Thingi10K 数据集上对称距离误差对比

为了测试算法的鲁棒性，作者在有噪声和残缺模型上比较了不同方法的结果，这两类模型在实际应用中经常遇到，特别是通过 3D 扫描设备扫描物体得到的模型。图5和图6分别展示了有噪声模型和残缺模型的检测结果，结果表明PRS-NET相比其他方法鲁棒性更高，对这类模型检测效果更好。

图5 有噪声模型对称性检测结果对比

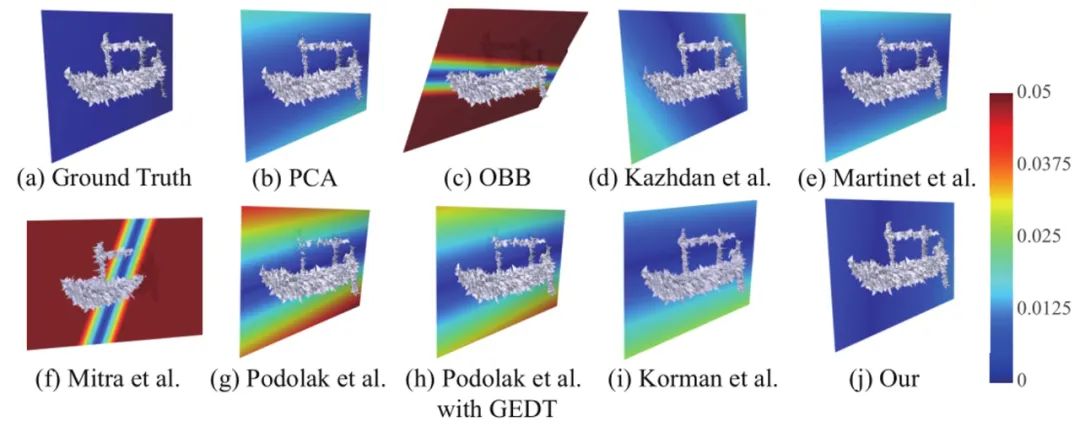
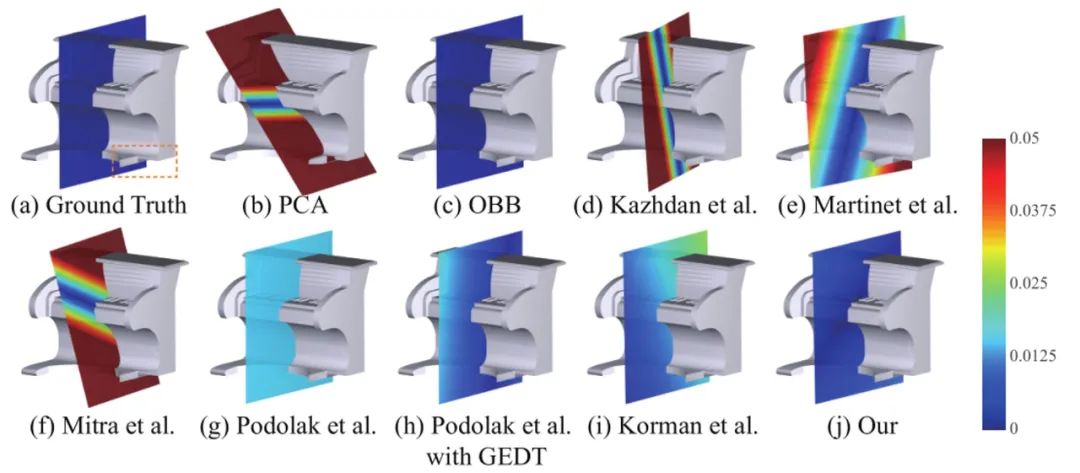
图6 残缺模型对称性检测结果对比

对称性分析可应用于模型补全，图7展示的模型补全结果中可以看到，PRS-NET和有向包围盒的方法得到了最好的补全结果。

图7 模型补全对比

Part3

Jittor开源，训练速度较Pytorch提升1.98倍

PRS-NET利用对称模型的特性提出了度量对称程度的可微损失函数，进而实现了无监督的网络训练，能准确高效的分析三维模型的对称性，并且得益于对具备多样性的三维模型的学习，PRS-NET相比其他方法也更加鲁棒。

该论文已发表在计算机图形学顶级期刊CCF A类期刊IEEE TVCG上。有关论文的更多细节，及论文、代码的下载，请浏览项目主页。

http://geometrylearning.com/prs-net/

Jittor 实现代码：

https://github.com/IGLICT/PRS-NET-Jittor

目前PRS-NET已经发布计图(Jittor) 版本的代码！Jittor是清华大学计算机系图形学实验室研发的一个全新的国产深度学习框架。

在Jittor框架的加持下，PRS-NET能够显著节省显存消耗，提高训练的效率。在相同的batchsize下，Jittor所需的显存空间仅为Pytorch版本的一半。在占据显存空间相当的条件下，Jittor的运行速度是Pytorch的1.98倍，能够在相同的条件配置下有效提升训练的效率。

参考文献

1. Michael Kazhdan, Bernard Chazelle, David Dobkin, Adam Finkelstein and Thomas Funkhouser. A Reflective Symmetry Descriptor. In European Conference on Computer Vision (ECCV), 2002.

2. Niloy J. Mitral, Leonidas J. Guibas and Mark Pauly. Partialand Approximate Symmetry Detection for 3D Geometry. ACM Transactions on Graphics (SIGGRAPH 2006), 25, 3 (2006), 29:1-29:9.

3. Joshua Podolak, Philip Shilane, Aleksey Golovinskiy, Szymon Rusinkiewicz and Thomas Funkhouser.  Planar-Reflective Symmetry Transform for 3D Shapes. ACM Transactions on Graphics(SIGGRAPH 2006), 25, 3 (2006), 30:1-30:11.

4. Lin Gao, Ling-Xiao Zhang, Hsien-Yu Meng, Yi-Hui Ren, Yu-Kun Lai and Leif Kobbelt. PRS-Net: Planar Reflective Symmetry Detection Net for 3D Models. IEEE Transactions on Visualization and Computer Graphics, 27,6 (2021), 3007 -3018.

GGC往期回顾

1. 计图支持寒武纪！动态图性能较PyTorch提升270倍

2. External Attention：计图团队提出两层线性层结构超越Self Attention

3. 计图开源：智能P图神器DeepFaceEditing

4. Computational Visual Media被SCI收录

5. Jittor开源：清华大学图形学实验室推出点云Transformer

您可通过下方二维码，关注清华大学图形学实验室，了解图形学、Jittor框架、CVMJ期刊和CVM会议的相关资讯。