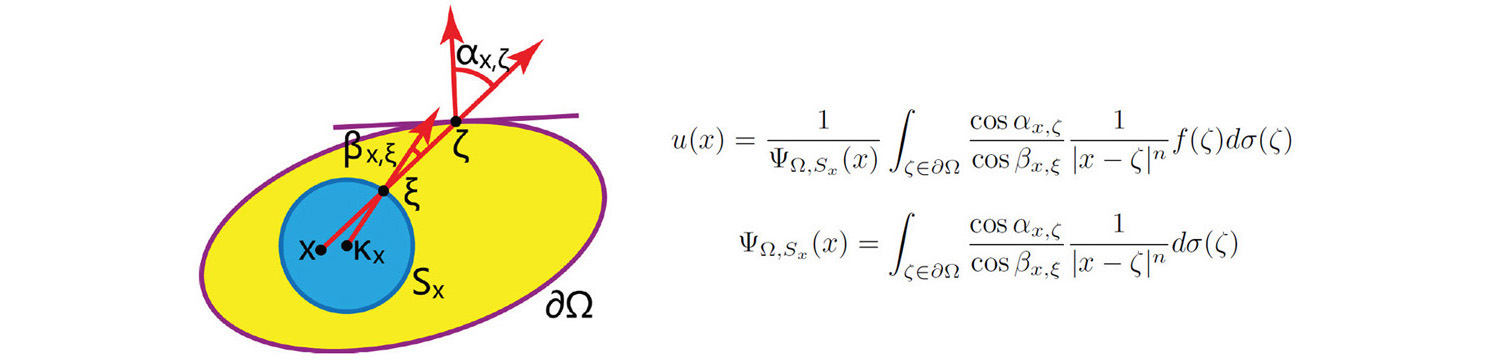
Poisson Coordinates

Harmonic functions are the critical points of a Dirichlet energy functional, the linear projections of conformal maps. They play an important role in computer graphics, particularly for gradient-domain image processing and shape-preserving geometric computation. We propose Poisson coordinates, a novel transfinite interpolation scheme based on the Poisson integral formula, as a rapid way to estimate a harmonic function on a certain domain with desired boundary values. Poisson coordinates are an extension of the Mean Value coordinates (MVCs) which inherit their linear precision, smoothness, and kernel positivity. We give explicit formulae for Poisson coordinates in both continuous and 2D discrete forms. Superior to MVCs, Poisson coordinates are proved to be pseudoharmonic (i.e., they reproduce harmonic functions on n-dimensional balls). Our experimental results show that Poisson coordinates have lower Dirichlet energies than MVCs on a number of typical 2D domains (particularly convex domains). As well as presenting a formula, our approach provides useful insights for further studies on coordinates-based interpolation and fast estimation of harmonic functions.

Poisson Coordinates [2.4M Paper] [3.2M Slides]

Xian-Ying Li, and Shi-Min Hu.

IEEE Transactions on Visualization and Computer Graphics, 2013, 19(2), 344-352.

@article {li2012poisson,
  author = {Li, Xian-Ying and Hu, Shi-Min},
  title = {Poisson Coordinates},
  journal = {IEEE Transactions on Visualization and Computer Graphics},
  year = {2013},
  volume = {19},
  number = {2},
  pages = {344-352},
}

Poisson coordinates are barycentric coordinates, which are the concept related to interpolating a function within a closed polygon using a linear combination expression of function values specified at polygon vertices; the coordinates (or weights) of this linear combination are called "barycentric" if they have linear precision (i.e., the interpolation reproduces linear functions).

Batrycentric coordinates for triangles were probable first studied by Giovanni Ceva (1648-1734) and August F. Mobius (1790-1868). However, barycentric coordinates for a general domain are not unique. Most recently, various barycentric coordinates for general domains in 2D and even higher dimensions have been proposed. For a full list of recent researches on general barycentric coordinates, please refer to: http://www.inf.usi.ch/hormann/barycentric/.